5.5.1 Versuche in "größeren" Höhen
5.5.2 Versuch von Trouton und Noble
5.5.3 Versuch von Champeney
Das Ergebnis des Michelson-Versuches erweckte den Anschein, daß die Erde den Äther vollständig mitführt. Man nahm nun an, daß vielleicht von der durch den Weltraum rasenden Erdkugel eine mehr oder weniger dicke Ätherschicht mitgerissen wird, so daß sich ein ,,Ätherwind" erst in größeren Höhen bemerkbar macht. Genannt werden in dem Zusammenhang ein 1925 durchgeführter Versuch im 1742 m ,,hoch" gelegenen Mount-Wilson- Observatorium und ein 1927 in ,,großen" Höhen durchgeführter Ballonversuch. Was kann von solchen Versuchen in unserem Sinne eigentlich erwartet werden?
Was sind in diesem Zusammenhang ,,größere" Höhen? Die Frage lautet auch: Welche quantitativen Bewegungen führt die latente Materie im Innern des Erdwirbels aus, und in welchen Höhen sind überhaupt meßbare Unterschiede dieser Bewegung zu erwarten?
Das ist allgemein die grundsätzliche Frage nach der Bewegung der Materie im Innern eines diskusförmigen Materiewirbels, der allseitig von außen nach innen abgebremst wird und folglich differentiell rotiert. Exakte Aussagen zu dieser Wirbelbewegung, die auch für die Luft- und Wasserwirbel noch zu erforschen sind, werden erst nach umfassenden Untersuchungen und Messungen möglich sein. Eine exakte mathematische Erfassung derartiger Bewegungsvorgänge wird einen ungerechtfertigt hohen Aufwand erfordern, folglich wird man sich auf zweckgerichtete Näherungen einzustellen haben (6). Wir begnügen uns deshalb zunächst im folgenden mit groben Näherungen und legen vorrangig Wert auf eine qualitative Aussage. Verwendete Zahlenwerte sollen nur die qualitative Aussage verdeutlichen helfen.
Der Wirkungsradius der Erde, in dem noch ,,Erdanziehungskräfte" nachweisbar sein sollen, wird mit etwa 900000 km angegeben. Diesen Radius wollen wir auch als Wirkungsradius des Erdwirbels der latenten Materie ansehen. Die genannten ,,größeren" Höhen liegen so gesehen noch immer ganz in der ,,Nähe" der Erdoberfläche. Über die Bewegung der latenten Materie im Innern des Erdwirbels lassen sich zunächst nur grobe Vermutungen anstellen. Die Natur beschert uns aber eine große Anzahl beachtenswerter natürlicher Experimente.
So bewegen sich z.B. alle Körper unseres Sonnensystems, mit wenigen Ausnahmen, in einer flachen Ebene, (Wirbel-Äquator-Ebene), um die Sonne.
Es ist denkbar, daß die Bahnen der Himmelskörper bereits seit ihrer Entstehung in dieser Ebene liegen, aber auch, daß sie erst im Verlaufe von Milliarden Jahren in diese Ebene hineingedreht worden sind. Es scheint so, daß alles, was im Bereich dieser einheitlichen Ebene geschieht, relativ beständig und gesetzmäßig abläuft.
Nach unserer Auffassung ist, wie schon mehrmals betont, die latente Materie an Entstehung und Bewegung der Himmelskörper und auch an der Aufrechterhaltung einer ihnen erteilten Bewegung aktiv und ursächlich beteiligt. Deshalb muß zwischen der Bewegung der Planeten und der latenten Materie um die Sonne ebenso ein gesetzmäßiger Zusammenhang bestehen wie zwischen der Bewegung der Satelliten und der latenten Materie um die Erde.
Aus dem Gravitationsparameter µ = Gm, wobei G die Gravitationskon stante und m die Masse der Sonne bzw. der Erde ist (4.3), ergibt sich die erforderliche Kreisbahngeschwindigkeit für einen Planeten bzw. Satelliten zu
![]() .
Dann ist r die Entfernung vom Rotationszentrum des Wirbels.
.
Dann ist r die Entfernung vom Rotationszentrum des Wirbels.
Der Gravitationsparameter µ wird seit Newton als eine Größe aufgefaßt, die die ,,Massenanziehungskraft" eines Himmelskörpers charakterisiert. In unserem Sinne ist µ eine Zustandsgröße des Wirbels der latenten Materie, die unabhängig davon ist, ob sich im Wirbelzentrurn eine kompakte Masse befindet oder nicht.
Man hat dem Wirbelzentrum eine Masse der Größe "zugeschrieben", die zur Übereinstimmung der berechneten Bewegungsabläufe mit den Beobachtungstatsachen erforderlich ist (4.3). Für die Erde bzw. für den Erdwirbel der latenten Materie errechnet man den Gravitationsparameter:
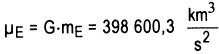
Damit lassen sich die erforderlichen Bahngeschwindigkeiten für einen Körper, der die Erde umläuft, in Abhängigkeit von seiner Entfernung r zum Erdmittelpunkt bzw. zum Wirbelzentrum berechnen.
Folgende Tabelle und die Darstellung 5.5.1-1
sollen auf die orientieren, die in ,,Nähe" der Erdoberfläche
zu erwarten sind.
|
r in km |
v in km/s |
r in km |
v in km/s |
h in km |
|---|---|---|---|---|
|
800 000 |
0,706 |
6978 |
7,558 |
600 |
|
700 000 |
0,755 |
6878 |
7,613 |
500 |
|
600 000 |
0,815 |
6778 |
7,669 |
400 |
|
500 000 |
0,893 |
6678 |
7,726 |
300 |
|
400 000 |
0,998 |
6578 |
7,784 |
200 |
|
300 000 |
1,153 |
6478 |
7,844 |
100 |
|
200 000 |
1,412 |
6388 |
7,89926 |
10 |
|
100 000 |
1,996 |
6387 |
7,89988 |
9 |
|
90 000 |
2,104 |
6386 |
7,90050 |
8 |
|
80 000 |
2,232 |
6385 |
7,90111 |
7 |
|
70 000 |
2,386 |
6384 |
7,90173 |
6 |
|
60 000 |
2,577 |
6383 |
7,90235 |
5 |
|
50 000 |
2,823 |
6382 |
7,90297 |
4 |
|
40 000 |
3,157 |
6381 |
7,90359 |
3 |
|
30 000 |
3,654 |
6380 |
7,90421 |
2 |
|
20 000 |
4,464 |
6379 |
7,90483 |
1 |
|
10 000 |
6,313 |
6378 |
7,90545 |
0 |
|
9 000 |
6,655 |
6000 |
8,151 |
|
|
8 000 |
7,059 |
5000 |
8,929 |
Tabelle 5.5.1-1: Die für einen Erd-Satelliten (theoretisch) erforderliche Kreisbahngeschwindigkeit.
Für die Berechnung des theoretischen
Kurvenverlaufes wird die Masse der Erde als punktförmig angenommen,
was für große Entfernungen unbedeutend ist. Aber auch für
die ,,Erdnähe" wird der theoretische Kurvenverlauf durch die tatsächliche
Bewegung künstlicher Himmelskörper noch gut bestätigt.
Ein Beispiel aus dem umfangreichen Tatsachenmaterial:
Für einen Flugkörper auf nahezu kreisförmiger Bahn in einer
Höhe von 500 km wird bei einem Neigungswinkel von 2,99" eine
Umlaufperiode von 94,49 min angegeben.
Die Bahnebene des Satelliten liegt also nahe der Äquatorebene, und
seine ,,Flughöhe" über der Erdoberfläche beträgt bei
dem in der Darstellung 5.5.1-1 verwendeten Maßstab nur einen
Millimeter. Für diese Höhe errechnet sich mit dem Radius r =
6878 km eine theoretische Bahngeschwindigkeit VK = 7,613 km/s. Für
die wirkliche
Bahngeschwindigkeit erhält man: ![]() .
.
Dadurch wird der theoretische Kurvenverlauf vorzüglich bestätigt (!).
Mit h ist in der Tabelle zusätzlich die Höhe über dem Erdäquator angegeben. (Erdradius am Äquator: 6378 km). In der Raumfahrt wird meistens die Höhe über dem mittleren Erdradius (6371km) genannt. Damit ergäbe sich z. B. in ,,Höhe" der Erdoberfläche eine Geschwindigkeit v 7,91 km/s und für eine Parkbahn in etwa 200 km Höhe v = 7,79 km/s.
Die Darstellung 5.5.1-1 enthält nur einen winzigen Ausschnitt1 knapp ein Hundertstel, der Ausdehnung des Erdwirbels. Um nur noch den Mond in der Darstellung unterzubringen, müßte die r - Achse bei dem gewählten Maßstab etwa 50-fach verlängert werden. Wir befinden uns also mit unserem Ausschnitt ganz in Erdnähe. Erstaunlich nur, wie das Krümchen Erde seinen "Massenanziehungsbereich" beherrscht. Man beachte in diesem Zusammenhang auch das erstaunliche Rechenexempel in (4.3).
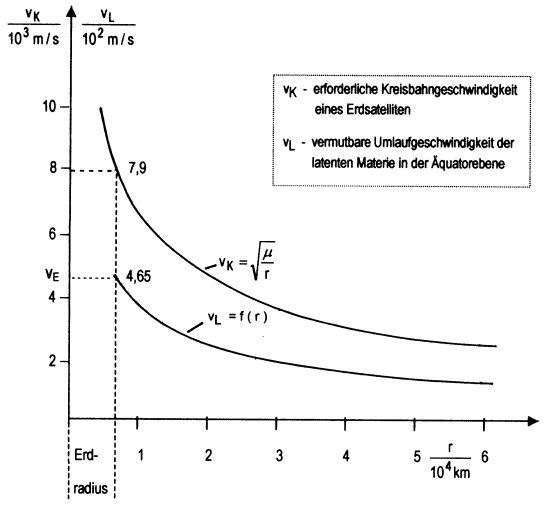
Bild 5.5.1-1: Darstellung vK
f(r) und vL f(r) für den Erdwirbel
Wir stellen fest:
Wie aus der Tabelle ersichtlich ist, ändert sich vK in Erdnähe auf 1 km Höhenunterschied um 62 cm/s.
Die Umfangsgeschwindigkeit der Erde am Äquator
beträgt bei der Rotationsperiode von 23 h, 56 min, 4s: vE
= ![]() rE = 2
rE = 2![]() nrE
= 0,4648 km/s.
nrE
= 0,4648 km/s.
Die Erdoberfläche hat keine bemerkbare oder bemerkenswerte Relativgeschwindigkeit zu der sie umgebenden latenten Materie, das hat der Michelson-Versuch bewiesen.
Für einen bestimmten Radius r ist folglich die Geschwindigkeit der latenten Materie bekannt: an der Erdoberfläche, bei h = 0, r= 6378 km, ist vE=vL.
Damit ergibt sich ein Verhältnis: ![]()
Läßt sich daraus auf die Bewegung
der latenten Materie schließen?:
Zunächst wären drei grundsätzliche Möglichkeiten in Erwägung zu ziehen: Die latente Materie im Abstand r vom Wirbelzentrum bewegt sich entweder mit größerer oder mit gleich großer oder mit kleinerer Geschwindigkeit als die durch sie ,,angetriebenen" Himmeiskörper.
Bei den zwei erstgenannten Möglichkeiten müßte die Geschwindigkeit der latenten Materie sprunghaft vom Wert VE = VL = 0,4648 km/s auf mindestens VK = 7,9 km/s ansteigen. Das ist aber unwahrscheinlich.
So liegt der Gedanke nahe, daß die latente Wirbelmatene langsamer rotiert als die durch sie ,,angetriebenen" Körper. Dies kann zunächst als ungewöhnlich empfunden werden, aber es gibt keine Veranlassung, daran zu zweifeln. Die Kraftwirkungen des Wirbels auf kompakte Körper sind nicht nur als ,,Strömungswiderstand" deutbar; sonst könnte es keine gegenläufige Bewegung geben. Erklärbar ist die Kraftwirkung im Wirbelinnern als Folge der Entstehung eines tangentialen und radialen Druckgefälles durch die differentielle Rotation des Wirbels.
Man möge diese Erscheinung mit dem
Auftrieb in Flüssigkeiten und in Luft vergleichen: Sogar im ruhenden
(!) Medium erfährt ein Körper durch das vorhandene Druckgefälle
eine Kraftwirkung (Auftrieb).
Wir gehen also davon aus, daß der
Geschwindigkeitsverlauf vL = f(r) der latenten Materie über
der Erdoberfläche qualitativ dem Geschwindigkeitsverlauf der umkreisenden
Himmelskörper vK = f(r) vergleichbar ist. Dividiert man
alle Werte der Kurve vK = f(r) durch 17, wobei hier dennoch
nur die qualitative Aussage betont sei, erhält man die in Bild
5.5.1-1 ebenfalls dargestellte Kurve vL = f(r).
Demnach ändert sich in Erdnähe
am Äquator die Geschwindigkeit der latenten Materie auf 1 km Höhenunterschied
um etwa 3,6 cm/s (!).
So gesehen waren die eingangs erwähnten
Versuche in einer ,,Höhe" von 1742 m und in Ballonhöhe, (10-20)
km, bei denen man bestrebt war, eine Relativgeschwindigkeit von 30 km/s
nachzuweisen, völlig aussichtslos. Bemerkenswert ist ein von Miller
1925 auf dem Mount Wilson durchgeführter Versuch. Im Gegensatz zu
den üblichen Mitteilungen, daß keiner der Ätherversuche
eine Relativgeschwindigkeit zum Äther nachgewiesen habe, berichtet
Delokarow, daß bei einer Wiederholung des Michelson-Versuches auf
dem Mount Wilson eine lnterferenzverschiebung gemessen wurde, die einer
Relativgeschwindigkeit der Erde zum Äther von etwa 10 km/s entspricht.
Die Gegner Millers hätten ihn jedoch verhöhnt und die wissenschaftliche
Bedeutung seiner Versuche in Frage gestellt. Vavilow soll dazu geäußert
haben: ,,In den Versuchen Millers muß man die Beobachtung von ihrer
Interpretation unterscheiden. Miller interpretierte den Effekt als Resultat
der Bewegung des ganzen Sonnensysterns. Das rief Zweifel hervor." <17>
Sicherlich ist bei derartigen Versuchen
die Möglichkeit örtlicher Anomalien in der Bewegung der latenten
Materie nicht auszuschließen. Diese wären als Ergebnis verschiedenster
materieller Wechselwirkungen, vergleichbar mit Luft- und Meeresströmungen,
durchaus erklärbar.
Zweifeln muß man an der wissenschaftlichen
Lauterkeit derjenigen, die solche gemessenen Tatsachen negieren, weil diese
nicht der Erwartung entsprechen oder nicht in eine vorherrschende Theorie
einzuordnen sind.
Versuchsanliegen:
In der Elektronentheorie (4.12.3)
deutet Lorentz, gestützt auf experimentelle Tatsachen, alle grundlegenden
Erscheinungen der Elektrodynamik als Ätherwirkung. Wenn es den absolut
ruhenden Ather gibt, wie es Lorentz annahm, und wenn die elektromagnetischen
Erscheinungen Ätherwirkungen sind, müßte ein elektrischer
Dipol (geladener Kondensator), wenn er sich mit konstanter Geschwindigkeit
und geradlinig gegenüber dem Äther bewegt, auf sich selbst ein
Drehmoment ausüben. Somit sollte zugleich die Bewegung der Erde gegenüber
dem ruhend angenommenen Äther nachgewiesen werden. Der Versuch ist
im Grundanliegen dem Michelson-Versuch vergleichbar und wird ebenfalls
als Fundamentalversuch der Relativitätstheorie bezeichnet, der speziell
die Gültigkeit des Relativitätsprinzips für die Kombination
Mechanik/Elektrodynamik nachweist.
Versuchsanordnung (Draufsicht):
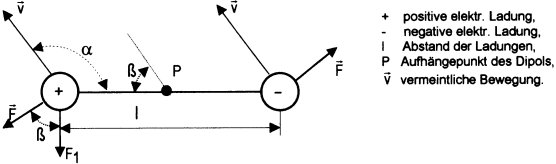
Bild 5.5.2-1: Trouton-Noble-Versuch
Versuchsprinzip:
Die Versuchsanordnung ist im Aufhängepunkt drehbar, aber ruhend gegenüber der Erde, aufgehangen. Sie bewegt sich, wie (irrtümlich) angenommen wurde, gemeinsam mit der Erde und v=30 km/s durch das ruhende ,,Äthermeer'. Die Versuchsanordnung ist um den Winkel ß gegenüber der (vermeintlichen) Bewegungsrichtung gedreht.
Gemäß dem Gesetz von
Biot-Savart ![]()
erzeugt die ,,bewegte" positive Punktladung,
(sofern sie sich tatsächlich in ihrem Wechselwirkungssystem bewegt),
am Ort der negativen Ladung die magnetische Feldstärke
![]() .
.
Die Richtung der erzeugten magnetischen
Feldstärke entspricht für die bewegte positive Ladung dem Bewegungssinn
der Rechtsschraube.
Gleichermaßen bewirkt die bewegte
negative Punktladung am Ort der positiven Ladung eine magnetische Feldstärke
von gleichem Betrag. Für die bewegte negative Ladung ist die erzeugte
magnetische Feldstärke dem Rechtsschraubensinn entgegengerichtet.
An beiden Orten durchsetzen also die magnetischen Feldlinien in der Darstellung
5.5.2-1 die Ebene gleichsinnig (von oben nach unten).
Auf eine im Magnetfeld bewegte Ladung wirkt die Lorentzkraft:
![]() ;
Betragsform: F = Q v B sin
;
Betragsform: F = Q v B sin ![]() .
.
Diese Kraft wirkt, wie in der Formel erfaßt
und im Bild dargestellt, recht winklig zur Bewegungsrichtung der Anordnung.
Da v und B stets senkrecht aufeinanderstehen,
(![]() = 90° und sin
= 90° und sin![]() = 1), gilt folglich F =Q v B = Q v µ0 H.
= 1), gilt folglich F =Q v B = Q v µ0 H.
Somit ergibt sich für die beiden
gleich großen Kräfte:
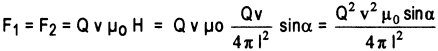
Jede der beiden Kräfte bewirkt, von
oben gesehen, ein linksdrehendes Drehmoment um den Punkt P:
![]()
Gesamtdrehmoment: Mges = 2 M
= F l cosß = ![]()
Mit a = 180° -ß , sin(180°- ß) = sin ß und sinß cosß = ½sin(2ß)
folgt:
Versuchsergebnis:
Es konnte mit dieser Versuchsanordnung
unter den genannten Annahmen und Versuchsbedingungen kein Drehmoment nachgewiesen
werden, obwohl das "Gesetz von Biot-Savart" und die "Lorentzkraft" durch
andere Versuche der Elektrodynamik vorzüglich bestätigt werden
und in Anwendung sind.
Das war ein Duell Lorentz gegen Lorentz!
Entweder sind die elektrornagnetischen Vorgänge keine Ätherwirkung,
oder es gibt gar keinen Äther, oder es gibt keinen absolut ruhenden
Äther.
Das Versuchsergebnis ist nicht verwunderlich! In anderen elektrodynamischen Versuchen und Anwendungen bewegen sich elektrische Ladungen tatsächlich in ihrer unmittelbaren stofflichen Umwelt. Bei diesem Versuch aber, wie bei den anderen Äthernachweis-Versuchen, hatte die Versuchseinrichtung keine Bewegung gegenüber dem Äther bzw. der latenten Materie. Es war v = 0 ! Damit ergibt sich praktisch und in obiger Formel kein Drehmoment.
In moderner Deutung sieht man in diesem Versuchsergebnis eine Bestätigung des "lnertialsystems" und des ,,Speziellen Relativitätsprinzips" (Gleichwertigkeit der Bezugssysteme), bei denen die Ursache einer Erscheinung nicht in der stofflichen Wechselwirkung, sondern "schlechthin' in einer beliebig wählbaren Relativbewegung gesehen wird.
Dieses Experiment ist eine 1963 durchgeführte Variante des Michelson Versuches.
Versuchsanordnung:
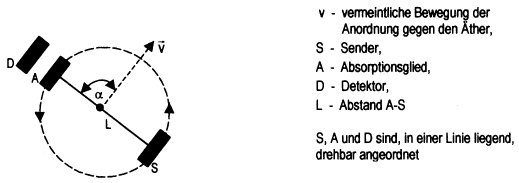
Bild 5.5.3-1: Versuchsaufbau von Champeney
Versuchsprinzip:
Laufzeitunterschiede der Signale des Senders
von 5 nach A, die bei der Bewegung der Anordnung gegen den Äther auftreten
würden, führen zu Frequenzänderungen ![]() fA
und wären in D registrierbar.
fA
und wären in D registrierbar.
Laufzeit der Signale von S nach A:
Mit den Voraussetzungen zum Michelson-Versuch
(5.1,
S.108) ergibt
sich:
![]() ;
; ![]() (Näherung
für v/c « 1).
(Näherung
für v/c « 1).
Die Laufzeit der Signale hätte demnach,
statisch betrachtet, für jede Winkeleinstellung![]() einen
anderen Wert.
einen
anderen Wert.
Rotieren S, A und D mit konstanter Winkelgeschwindigkeit ![]() ,
ergibt sich eine zeitabhängige Laufzeit der Signale:
,
ergibt sich eine zeitabhängige Laufzeit der Signale:
![]()
Bei Rotation der Anlage müßte sich folglich die Laufzeit der Signale, d. h. ihr zeitlicher Signalabstand, ändern, und die in A durch D beobachtbare Frequenzänderung wäre der Laufzeit proportional.
Laufzeitänderung: ![]()
Frequenz der in A eintreffenden Impulse: ![]()
Damit ergibt sich ein zu erwartendes
Frequenzverhältnis: ![]()
Diese Frequenzänderung wird in der Versuchsanordnung durch Ausnutzung des Mößbauereffektes im Detektor zur Anzeige gebracht. Der Mößbauereffekt hat für das Prinzip des Versuches keine Bedeutung. Er dient hier lediglich als Mittel zum Zweck der Anzeige des erwarteten Ergebnisses, weil er insbesondere zur Messung sehr kleiner Frequenzänderungen vorzüglich geeignet ist.
Für diese Versuchsanordnung wurde
ein Verhältnis v/c = 10-10 noch als nachweisbar angesehen.
Versuchsergebnis:
Es konnte in diesem Versuch keine Frequenzänderung und folglich auch kein Laufzeitunterschied festgestellt werden. Durch die Längenkontraktion allein ist das Ergebnis nicht erklärbar. Das Versuchsergebnis gilt heute neben dem Michelson-Versuch als Bestätigung der Einstein'schen Hypothese von der ,,Konstanz der Vakuumlichtgeschwindigkeit".
In unserer Deutung besagt auch dieses Versuchsergebnis, daß es am Ver suchsort keine Relativgeschwindigkeit zwischen der Versuchseinrichtung und der latenten Materie gegeben hat. In obiger Formel war in Wirklichkeit v = 0! Das ist ausführlich erläutert in (4.11) u. (5.4). In diesem Versuch wurde nur ,,bewiesen", daß bei v=0 auch fA=fS ist.
Damit sei die Betrachtung der Versuche beendet, deren vielfältige Deutung stets nur Interpretation ihres ,,Schweigens" war und ist. Ob es nicht doch eine Möglichkeit gibt, diese stummen, hochpräzisierten Versuchsapparaturen zu einer aktiven Antwort auf die durch sie an die Natur gerichteten Anfragen zu bewegen ?
Inhalt
<< (5.4) Neue
Deutung des Michelsonversuchs
>> (5.6) Wie man den
Michelson-Versuch durchführen muß