Spur eines Jahrhundertirrtums

6 Um eine qualitativ neue Deutung der ,,Gravitation"

Die Wirbelauffassung sieht die "Gravitation" nicht als Massenanziehungskraft". Und so ist es naheliegend und verlockend, die Druck- und Kraftwirkungen in differentiell rotierenden Wirbeln der latenten Materie, die nach dem Wirbelprinzip Ursache der Gravitation sind, auch mathematisch zu erfassen.

Mit der Vielfalt von Wirbeln und der Berechnungsmöglichkeiten ihrer Erscheinungsformen und Wirkungen befaßt man sich seit einigen hundert Jahren. Eine allgemeingültige Wirbeltheone wäre ein undurchschaubares Gewirr partieller Differentialgleichungen mit vielen Zusatzbedingungen und praktisch nicht zu gebrauchen, so daß man von vornherein nach vereinfachten und anwendbaren Modellen fragt. Zudem verbindet sich mit dem Begriff ,,Wirbel", vielfach berechtigt, ein scheinbar chaotisches, unerfaßbares Durcheinander, in dem ohnehin Theorie und Wirklichkeit nicht in Übereinstimmung zu bringen sind. Wer berechnet schon das Wettergeschehen oder die im Innern eines Tornados oder Wasserstrudels auftretenden Wirkungen? So entstanden spezielle Wirbeltheorien, die unter ganz bestimmten Prämissen gelten und für den Einzelfall zurecht gemacht sind.

Für unseren diskusförmigen Wirbel, der rings von Materie umgeben ist und der zudem als Wirbel in Wirbeln dem Einfluß eines übergeordneten Wirbelsystems unterliegt, gibt es keine vorgefertigte Lösung. In der Ebene des Wirbeläquators unseres Sonnensystems geht es jedoch auffallend gesetzmäßig zu. Deshalb seien an diesem Beispiel wenigstens unsere gute Absicht und die Unzulänglichkeit derartiger Bemühungen und Ergebnisse als Denkanregung angedeutet. Das hier verfolgte Grundanliegen sei an einer vereinfachten, noch überschaubaren Betrachtungsweise dargestellt, die unserem Spezialfall zumindest prinzipiell nahekommt.

Es wurde bereits betont, daß ein Wirbel der latenten Materie, der rings um von "ruhender" Materie umgeben ist, allseitig von außen nach innen abgebremst werden muß. Der Wirbel ist in dem Sinne vergleichbar mit der in der Literatur definierten "Drehströmung über festem Grund".

Zur Drehströmung über festem Grund:

"Bei den in großen Abständen von der Wand (vom festen Grund) umlaufenden Teilchen besteht Gleichgewicht zwischen der Zentrifugalkraft und dem radialen Druckgradienten. Die in Wandnähe in ihrer Geschwindigkeit abgebremsten Teilchen stehen unter dem gleichen nach innen gerichteten radialen Druckgrad ienten, während ihre Zentrifugalkraft wesentlich abgemindert ist. Auf diese Weise ergibt sich also in Bodennähe eine radiale Einwärtsströmung und aus Kontinuitätsgründen in axialer Richtung eine aufsteigende Strömung. Eine solche in der Grenzschicht entstehende Strömung, deren Richtung von derjenigen der Außenströmung abweicht, wird allgemein als Sekundärströmung bezeichnet. Die geschilderte Sekundärströmung bei der Strömung über festem Grund kann man sehr deutlich in jeder Teetasse beobachten: nachdem man die Drehströmung durch star kes Rühren erzeugt hat und dann die Strömung sich selbst überläßt, bildet sich nach kurzer Zeit in Bodennähe eine radiale Einwärtsströmung aus. Dieses erkennt man aus dem Ansammeln der Teeblättchen in der Mitte des Bodens der Teetasse." <58>

Bei der mathematischen Behandlung wird in <58> davon ausgegangen, daß die Flüssigkeit in großem Abstand von der Wand (von festem Grund) wie ein starrer (1) Körper mit der Winkelgeschwindigkeit  rotiert, womit unserem differentiell rotierenden Wirbel zunächst eine wesentliche Eigenschaft unterschlagen wird.

Durch Ableitung aus den Navier-Stokes'schen Gleichungen erhält man den radialen Druckgradienten für die in großem Abstand vorhandene reibungslose Strömung:

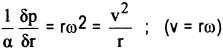
"Im Rahmen der Grenzschichttheorie nimmt man an , daß dieser Druckgradient auch in der von der Reibung beeinflußten Schicht in Wandnähe vorhanden ist." <58>

Bezogen auf den latenten Materiewirbel ist der ,,feste Grund" der Außenbereich der nördlichen bzw. südlichen Wirbelhälfte, in dem die rotierende in die relativ ruhende latente Materie übergeht; als ,,großer Abstand von der Wand" ist die Ebene des Wirbeläquators anzusehen. Dazu steile man sich den Wirbel am Äquator ·aufgeschnitten" und die Wirbelhälfte gewissermaßen als Gefäß vor, in dem die Materie rotiert.

v ist in unserem Falle die Kreisbahngeschwindigkeit der latenten Materie im Abstand r vom Wirbelzentrum, die wir mit v_k,L bezeichnen möchten.

In der Ebene des Wirbeläquators bewegen sich die Planeten und andere Himmelskörper differentiell mit einer theoretischen Kreisbahngeschwindigkeit v_k gemäß der Beziehung

G - Gravitationskonstante
M - Masse der Sonne
r - Bahnradius

Die "Sonnenmasse" M ist für die Wirbelauffassung nur eine Rechengröße, die im Newton'schen Denksystem der Sonne "zweckmäßig" zugeschrieben wurde und praktisch durch die Himmelsmechanik erwiesen ist.

Bisherige Erkenntnisse führten zu der Annahme, daß die Umlaufgeschwindigkeit der latenten Materie v_k,L kleiner ist als die der durch sie beeinflußten Körper.

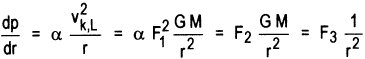
Nur zur besseren Übersichtlichkeit in der weiteren Darstellung wurde hier gesetzt: F₃ = F₂ G M und F₂ =  F₁².
ist, formell übertragen, die Dichte der latenten Materie. Es wäre zu er gründen, ob es physikalisch sinnvoll ist, eine solche Größe zu definieren oder ob erst die Kombination verschiedener Faktoren zu einer physikalisch sinnvollen Aussage führt.
Die zum Wirbelzentrum gerichtete Radialbeschleunigung a der Himmelskörper ist folglich proportional dem ebenfalls zum Zentrum gerichteten radialen Druckgradienten dp/dr:

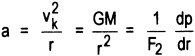
Integration ergibt qualitativ den Verlauf des Druckes im Wirbel der latenten Materie als Funktion der Entfernung vom Wirbelzentrum:

K ist deutbar als Druck der relativ ruhenden latenten Materie, der außerhalb des Wirbels vorhanden ist.

Die folgende Darstellung zeigt v_k = f(r) des Sonnenwirbels (auszugsweise), den Verlauf der Radialbeschleunigung a, der qualitativ auch dem des radialen Druckgradienten dp/dr entspricht und qualitativ den Verlauf des Druckes, der mit dem Radius ansteigt und schließlich in einen Wert des Umgebungsdruckes übergehen muß.

Man beachte, daß der Wirkungsradius des diskusförmigen Sonnenwirbels in der Ebene des Wirbeläquators mit mindestens 50 AE angenommen werden kann. In Richtung der Pole werden seine Wirkungen oder eine behauptete ,,Massenanziehungskraft" der Sonne schon in sehr viel geringerer Entfernung vom Zentrum nicht mehr wahrgenommen.

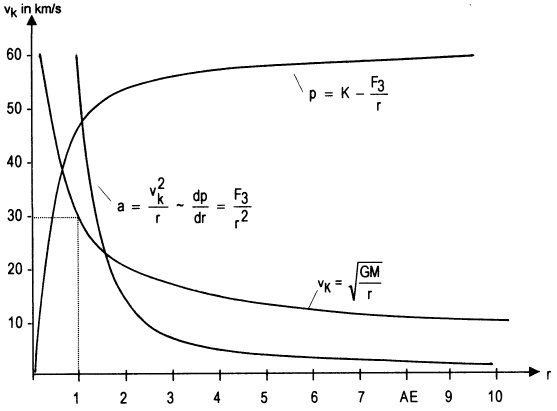
Bild 6-1: kenngrößen des Sonnenwirbeis zur Erklärung der Gravitation

Nun verfügen wir über drei Modellvorstellungen zur ,,Gravitation":
 

1. 1. Der zum Wirbelzentrum gerichtete Druckgradient bewirkt auf einen im Wirbel befindlichen Körper eine zum Wirbelzentrum gerichtete Kraft. In dieser Denkweise ist nur die Ebene des Wirbeläquators ein stabiler Wirkungsbereich. Allgemein werden Kraftwirkungen auf den Körper nicht nur durch seinen Abstand vom Wirbelzentrum bestimmt, sondern auch durch seine Richtung zum Wirbelzentrum. Pluto umkreist in der Ebene des Wirbeläquators das Zentrum mit dem Bahnradius 35 AE; in einer Bahnebene mit 900 Neigung wird kein Himmelskörper aus dieser Entfernung dem Einfluß des Sonnenwirbels unterliegen. Nur in der "Nähe" des Wirbelzentrums werden die Wirkungen aus lokalen "Kontinuitätsgründen" annähernd richtungsunabhängig sein. Eine Kontinuität der Wirkungen über den gesamten Innenbereich des Wir bels ist gar nicht zu erwarten. Gesteht man dem Außenbereich des flachen Wirbels ringsum etwa den gleichen Umgebungsdruck zu, so ist leicht einzusehen, daß der Ubergang in den Umgebungsdruck in Nord- Süd-Richtung auf sehr viel kürzerem Wege stattfindet und somit hier der radiale Druckgradient größer sein muß als in der Äquatorebene. Dann ist noch zu beachten, daß real keine punktförmigen ,,Massen" untereinander in Wechselwirkung stehen. Hier wechselwirken Wirbel noch unbekannter Ausmaße innerhalb übergeordneter Wirbel.

Eine exakte mathematische Erfassung dieser Wirbelwirkungen wäre, obwohl diese Denkart der Wirklichkeit vermutlich am weitesten nahekommt, sehr aufwendig bis unmöglich, das dazu erforderliche Formelwerk praktisch nicht zu gebrauchen, also ungerechtfertigt. Das bedeutsamste Merkmal dieser Denkweise: Die Gravitation wird von der physikalischen Ursache her gesehen und erfaßt. Die Kraftwirkung hat ihre Ursache in der Wirbelrotation, sie benötigt keinen Zentralkörper des Wirbels, keine Masse, von der eine andere Masse zum Mittelpunkt des Wirbels ,,hingezogen" werden müßte.
2. Die zweite Vorstellung, eine Zwischenlösung, sieht die Gravitation durch eine ihrer Erscheinungen. In F = ma = m 4²C/r², siehe (4.3), ist die Radialbeschleunigung a, die sich mit dem 3. Kepler'schen Gesetz nur als ,,Beobachtungstatsache" ergibt, noch unabhängig von den Eigenschaften der Sonne oder eines Planeten. Die Ursache dieser Erscheinung blieb zunächst ungeklärt. Erst Newton ,,macht" für die Radialbeschleunigung die Sonne verantwortlich. So hat man die Ursache der Erscheinung ,,Radialbeschleunigung" der Sonne ,,zugeordnet", weil weit und breit im leeren Raum keine andere Ursache zu erkennen war.
3. Die geläufigste Modellvorstellung über die Gravitation als "Massen- Anziehungs-Kraft" ist



Über Entstehung, Besonderheiten und Unzulänglichkeiten dieses "allgemeinen Gravitationsgesetzes" siehe (4.3)!
Das ,,Gesetz der Massenanziehungskraft" im leeren Raum ist Fundament der Allgemeinen Relativitätstheorie und des modernen physikalischen Weltbildes. Seine folgenschwere Besonderheit liegt noch darin, daß man die "Massenanziehungskraft" nicht als Modell, sondern als physikalische Realität ansieht. Die irreführenden Illusionen, die sich so ergeben und an deren vermeintlicher Erkenntnisfunktion sich viele berauschen, muß man zertrümmern: Die Welt wird nicht durch sich anziehende Massen zusammengehalten und reguliert, sondern durch Wirbel der latenten Materie.
Die ,,Massenanziehungskraft" mag als Modellvorstellung, da man nun über Jahrhunderte den himmlischen Wirbelzentren die ,,zweckerfüllenden" Massen zugeordnet hat, weiter die nützlichste sein und bleiben. Als Modell muß diese Auffassung jedoch von vielen Theoretikern erst noch anerkannt und gehandhabt werden, denn erster und wichtigster Grundsatz des Modelldenkens und des wissenschaft lichen Umgangs mit wissenschaftlichen Modellen ist:
Obwohl und weil wir wissen, daß die Wirklichkeit ganz anders und viel komplizierter ist, tun wir zweckmäßigso , als ob ... und beachten dabei aber die Grenzen der Aussagefähigkeit des Modells.

Womit wir wieder am Ausgangspunkt der "Spur ..." angelangt wären, aber um eine wesentliche Erkenntnis reicher sind.

Inhalt
<< (5.7) Der "Faserkreisel" ersetzt den Michelson-Versuch
>> Nachwort: Irrungen eines "Ballonfahrers"