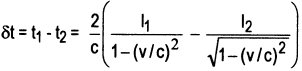
Der irische Physiker Fitzgerald veröffentlichte 1892 eine Hypothese, die Lorentz, um "seinen" ruhenden Äther zu retten, sofort annahm und ausbaute.
Lorentz ,,erklärte" das unerwartete
Ergebnis des Michelson-Versuches durch einen mysteriösen bis heute
unerklärlichen Vorgang: Der in Bewegungsrichtung der Erde liegende
Arm
der Michelson1schen Versuchsapparatur
soll sich verkürzen, wodurch der erwartete Laufzeitunterschied der
beiden Lichtstrahlen gerade kompensiert wird.
Für die erwartete Zeitdifterenz 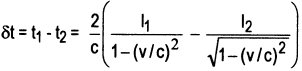
muß für ![]() t
= 0 erfüllt sein:
t
= 0 erfüllt sein: 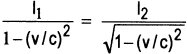
Daraus folgt durch elementare Umstellung: ![]()
Da ursprünglich l1 = l2
angenommen war, stimmt diese Gleichung nur, wenn sich l1 gegenüber
der angenommenen "Ruhelänge" verkürzt hat.
Und Lorentz verallgemeinert: Alle Körper
und Maßstäbe verkürzen sich in einem gegenüber dem
ruhenden Äther mit der Geschwindigkeit v bewegten Koordinatensystem
um den
Verkürzungsfaktor ![]() .
.
Damit soll nun verallgemeinert gelten: ![]()
Darin ist l0 die Länge des ruhend gedachten Stabes, l' die durch die Bewegung verkürzte Länge. Durch die nun angenommene Verkürzung des Armes ergeben sich wunschgemäß gleiche Laufzeiten der beiden Streustrahlen, t1 = t2.
Lorentz erklärt die Kontraktion als
Wirkung des ruhenden Äthers auf den bewegten Körper. Das mag
etwa mit der Deformierung eines Schwammes vergleichbar sein, der durch
eine
,,ruhende" Flüssigkeit bewegt wird.
Ein derartiger ,,Schwamm" dürfte aber nur wenn er geschoben wird,
eine Kontraktion erfahren; wenn er gezogen wird, müßte er gedehnt
werden.
Nach der Lorentz'schen Kontraktionshypothese
sind alle Körper, unabhängig von ihrer Beschaffenheit,
im selben Maße verkürzt , wenn sie sich mit gleicher
Geschwindigkeit
gegenüber dem Äther bewegen.
Trotz aller Ungereimtheiten: Der Lorentz´sche
absolut ruhende Äther und damit die Elektronentheorie waren zunächst
gerettet. Mit der Kontraktionshypothese "beweist" Lorentz die
Existenz des Äthers. Einstein "beweist"
mit dieser Hypothese die Nichtexistenz des Äthers II(1.6).
Entgegen irreführenden Formulierungen,
denen man begegnet, sei betont, daß die Kontraktionshypothese nicht
aus den Lorentz'schen Transformationsgleichungen sondern aus einem
speziellen Versuchsaufbau zur Erklärung
eines erwarteten, aber nicht eingetretenen Ergebnisses hervorgegangen ist.
Andere Versuchsaufbauten, die mit gleicher Absicht verwendet
wurden, führen nicht zu der "Erkenntnis",
daß sich Längen in Bewegungsrichtung des Systems verkürzen
müßten; wohl aber zur Erkenntnis v = 0, die aus allen anderen
Versuchen zum
beabsichtigten Äthernachweis hervorgeht
und die auch unserer Auffassung entspricht.
Die Lorentz'sche Lorentztransformation
Die seltsame Überschrift soll darauf
aufmerksam machen, daß man heute unter dem Begriff ,,Lorentztransformation"
etwas anderes versteht, als es Lorentz seinerzeit gemeint hat. Die
Lorentz'schen Gedanken zur Entstehung
seiner Transformationsgleichungen lassen sich leicht nachvoll ziehen. Man
möchte diese Gedanken und Absichten verstehen, um sie nicht mit
der späteren Nutzung und Deutung
der "Lorentztransformation" durch Einstein zu verwechseln, II(1.6). Einstein
nutzt die gleiche Formel, was im Modelldenken durchaus üblich ist.
Wenn aber das Modell die physikalische
Wahrheit zu repräsentieren beansprucht, möchte man sehr hell
hörig auf die dem Formelsystem unterschobenen Deutungen lauschen.
Nach der Galilei-Transformation lassen
sich die Koordinaten eines ruhenden Systems (S) in die eines bewegten Systems
(S') umrechnen und umgekehrt. Dies sei einleitend gezeigt,
wobei zur Anschaulichkeit die Betrachtung
nur für die x-Koordinate durchgeführt werden soll:
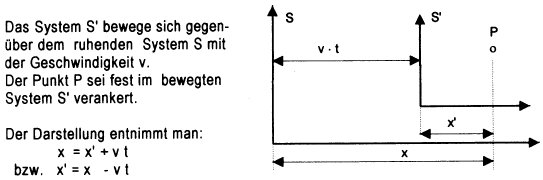
Bild 5.3.-1: Galilei-Transformation
Lorentz ergänzte mit seinen Auffassungen
die Galilei-Transformation so, daß im System S' eine Verkürzung
der Maßstäbe gegenüber dem gedachten Ruhezustand zum Ausdruck
kommt:
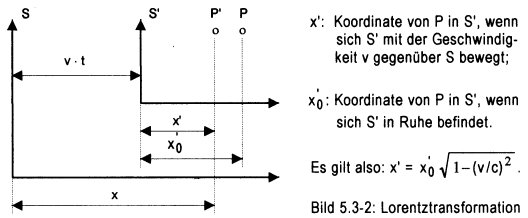
Bild 5.3-2: Lorentztransformation
Im System S' ist der Abstand x'0,
mit den Maßstäben des ,,unverkürzten" Systems S gemessen,
auf den Wert x' verkürzt worden, was in S' wegen der gleichzeitig
verkürzten Maßstäbe
nicht verspürt wird.
Mit den Maßstäben des Systems
S wird der Abstand x' als ![]() gemessen, also:
gemessen, also: ![]() bzw.
bzw. 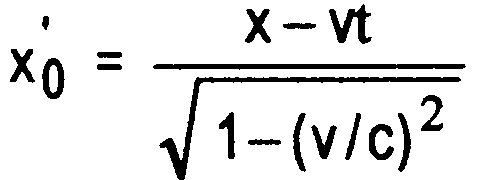
Ein in x = 0 zur Zeit t = 0 ausgelöster
Lichtblitz hat zur Zeit t in S den Weg x = ct und in S' den Weg ![]() zurückgelegt. An den geschrumpften Maßstäben in S' ist
folglich ein größerer Meßwert,
zurückgelegt. An den geschrumpften Maßstäben in S' ist
folglich ein größerer Meßwert, ![]() ablesbar.
ablesbar.
Nach Lorentz ist die Lichtgeschwindigkeit c gegenüber dem lichttragenden Äther (S) konstant und unabhängig von der Bewegung der Quelle. Deshalb hat das Licht in S nach der Zeit t die Strecke x = ct zurückgelegt, und deshalb hat es gegenüber dem bewegten System S' die Relativgeschwindigkeit c-v bzw. c+v. Hier wird die Lichtausbreitung im Äther noch analog zur Schallausbreitung in Luft aufgefaßt und behandelt.
Lorentz kann folglich keinesfalls als Wegbereiter der Relativitätstheorie angesehen und verdächtigt werden. Er ,,benötigte" den ruhenden Äther als Fundament seiner anerkannten Elektronentheorie. Ihm genügte es, eine Möglichkeit gefunden zu haben, mit der sich das Ergebnis des Michelson Versuches und der ruhende Äther in Einklang bringen ließen.
Lorentz verteidigte bis zuletzt, (gegen die Auffassungen Einsteins), die hypothetische Möglichkeit des absolut ruhenden Äthers und einer absoluten Zeit. Noch 1913 äußerte er: "Wie dem auch sei, aber diese Theorie - (die Theorie des unbeweglichen Äthers) - ist in ausreichendem Grade hoffnungsvoll und befriedigt mich völlig, denn sie zwingt nicht zu einer radikalen Überprüfung unserer Vorstellungen." <17>
Trotz ihrer inneren Widersprüche und Halbheiten zeichnet sich die Kontraktionshypothese durch einige bemerkenswerte Besonderheiten aus, die diese Hypothese und den in ihr enthaltenen Verkürzungsfaktor nahezu in den Rang einer ,,Zauberformel" erheben. Fassen wir die ,,zauberhaften" Eigenschaften der Kontraktionshypothese abschließend kurz zusammen:
Die Kontraktionshypothese "erklärt" das Ergebnis des Michelson-Versuches und ,,beweist" damit (für Lorentz) die Existenz des ruhenden Äthers.
Die Kontraktionshypothese mit ihren ,,neuen" Umrechnungsbeziehungen zwischen den Systemkoordinaten ändert an der Galilei-Transformation bei üblichen Geschwindigkeiten überhaupt nichts. Beträgt v ,,nur" 10 % der Lichtgeschwindigkeit, das sind 30000 km/s oder 108 Mill. km/h, so erhält man den Verkürzungsfaktor von 0,995.
Beim heutigen Stand der Technik und seinen
kühnsten Entwicklungsprognosen dürften Fahrzeuge mit derartigen
Geschwindigkeiten, ja selbst Geschosse, ins Reich der Utopie gehören.
Für einen Raumflugkörper, der z. B. mit v = 10 km/s die Erde
umkreist, ist die errechenbare Verkürzung praktisch nicht bemerkbar
und nicht bemerkenswert. Bei 50 % der Lichtgeschwindigkeit wäre der
Verkürzungsfaktor 0,866.
Man kann daher mit Berechtigung sagen,
daß die Kontraktionshypothese faktisch nicht störend wirkt und
keiner Berücksichtigung bedarf.
Die hypothetische Längenkontraktion muß als nicht nachweisbar angesehen werden. Da sich in einem bewegten System die mitbewegten Maßstäbe ebenfalls verkürzen sollen, ist die Verkürzung in einfacher Form nicht feststellbar, so daß kaum Widersprüche mit der Erfahrung zu erwarten sind. Die Hypothese wurde zur Rechtfertigung der Ergebnisse des Michelson-Versuches geschaffen, sie kann durch ähnliche Versuche nicht widerlegt, sondern nur bestätigt und bei entsprechen der Deutung ,,bewiesen" werden.
Mit der Kontraktionshypothese läßt sich vieles behaupten und deuten, aber nichts beweisen. Sie bietet sich somit als Ausgangspunkt für neue unbeweisbare Theorien an. Dabei gab es beim Michelson-Versuch, dem Ursprung dieser Hypothese, sicherlich gar keine Relativgeschwindigkeit v und folglich überhaupt keine Kontraktion.
Inhalt
<< (5.2) Herkömmliche
Deutungen des Versuchsergebnisses
>> (5.4) Neue Deutung
des Michelsonversuchs